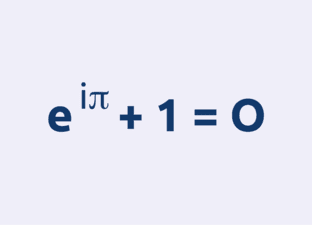Deze module is een vervolg op de module ‘Complexe getallen deel 1’. In deze module, geschikt voor wiskunde d op vwo, komt een uitbreiding van complexe getallen aan bod. Je leert in deze module twee nieuwe manieren om complexe getallen te noteren. Met deze nieuwe notaties leer je op een handige manier berekening met complexe getallen uit te voeren. Verder leer je met behulp van de formule van Euler complexe vergelijkingen op te lossen en je zult ontdekken dat een complexe wortel meerdere uitkomsten heeft in de verzameling van complexe getallen.
INHOUD:
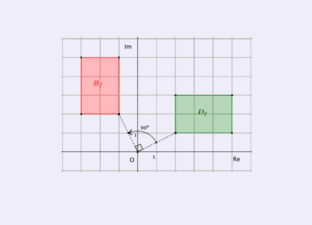
- Poolcoördinaten
- De polaire notatie van een complex getal
- De stelling van De Moivre
- De vergelijking zn = a + bi oplossen
- De formule van Euler
- Berekeningen meet de formule van Euler
- Vergelijkingen oplossen met de formule van Euler
- Diagnostische toets